【Python Coding】seabornで散布図を作る方法を解説します

こんにちは、TAKです。
前回に引き続き、今回もpythonのseabornを使った可視化について解説していきます。
今回は「Scatterplot(散布図)」について、pythonのJupyter Notebookを用いて紹介していきます。
1. pythonを用いた可視化方法を学んでいきたい方
2. pythonを用いて「散布図」を描けるようにしたい方
seabornを用いたデータ可視化 | Scatterplot
必要ライブラリのインポート

今回必要となるライブラリは以上の3つです。
前回までの記事でも毎回登場している「データ読込&可視化用のお馴染みのコード」です。
初回の記事で上記ライブラリの簡単な説明をしているので、今一つわからない方は以下の記事を参考にしてみてください。
利用データの確認
今回は、Kaggleでも公開されているデータを使用します。
データ内容は、保険加入者の属性(年齢・性別・BMI・喫煙習慣等)に基づいた保険料を示したものです。
下記でデータ読込結果を表示しているので、そちらを参照してイメージを深めてみてください。
データの準備
実際にpandasのread_csvを用いてデータセットとして読み込んでいきます。
csvファイルを読み込み、対象データの先頭5行を表示させているのが以下のコードです。
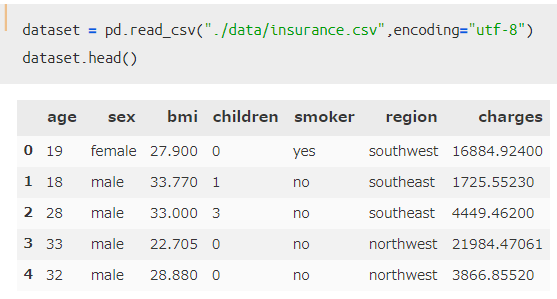
一番右のカラム「charges」が保険料金を表していて、それより左側のカラムが加入者の属性を表しているようなデータセットです。このデータを用いて可視化していきましょう。
データ可視化①
では実際にseabornを用いて散布図を描画していきましょう。
散布図は2変量データ(数値×数値)の可視化に向いている方法なので、数値変数(量的変数)を2つほどセレクトします。今回は、「BMI」と「Charges」の関係性について見ていくことにします。
僕は特徴量の手打ちが面倒なので、以下のようにしてリスト化しておきます。

そして、以下のコードを実行することで、散布図を描画することが可能です。
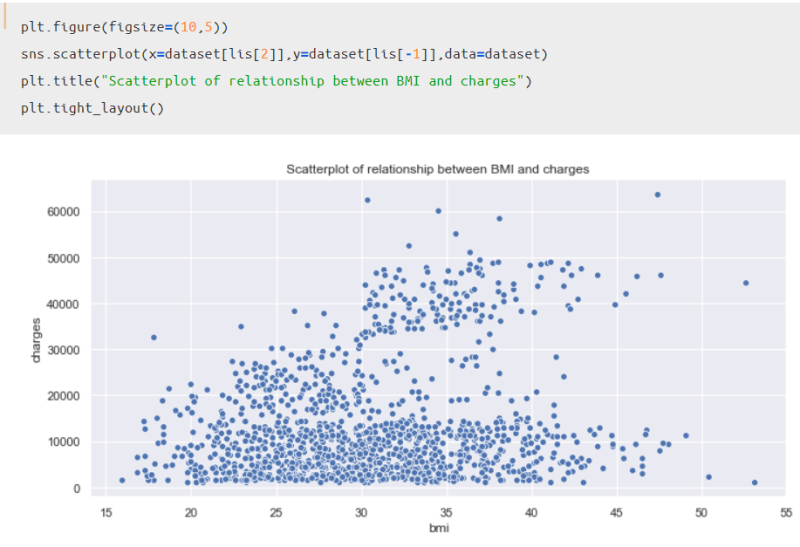
ポイントは以下2つです。
● 引数としてxとyの値、そして対象となるデータを指定する必要がある
これで散布図を描くことが出来ましたね。
パッと見た感じ、BMI指数の上昇に伴いChargeが上昇している人がいる一方で、あまり変化していない人もいるといった印象ですね。
この印象を確認するため、上記散布図に回帰直線を引く方法もあわせて紹介しておきます。
BMI指数とChargeがどの程度比例の関係にあるかをざっと把握することが可能になります。
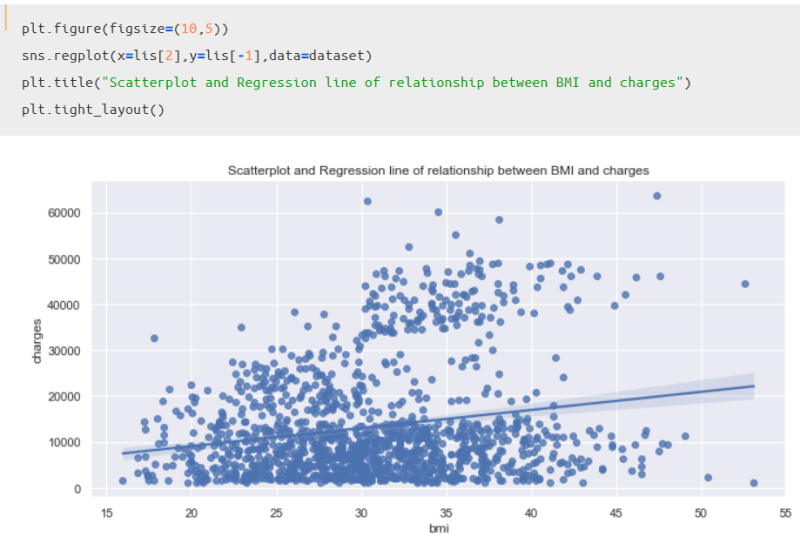
ある程度正比例の関係にあるので、BMI指数が上がればChargeも上がる傾向にあると言えそうです。
ただ、このデータは「性別」や「喫煙者・非喫煙者」といった情報を分けずにごちゃ混ぜの状態で表示しているため、これを内訳ごとに分けてみたいと思います。
データ可視化②
先ほどと同じデータを用いて、「性別」や「喫煙者かどうか」の属性を考慮した上で散布図を描画してみたいと思います。内訳を追加するためには、引数「hue」にカラム名を追加するだけでOKです。
まず、男女別に分けて表示した結果が以下です。
この結果を見る限り、男女間で明確な違いはあまりなさそうですね。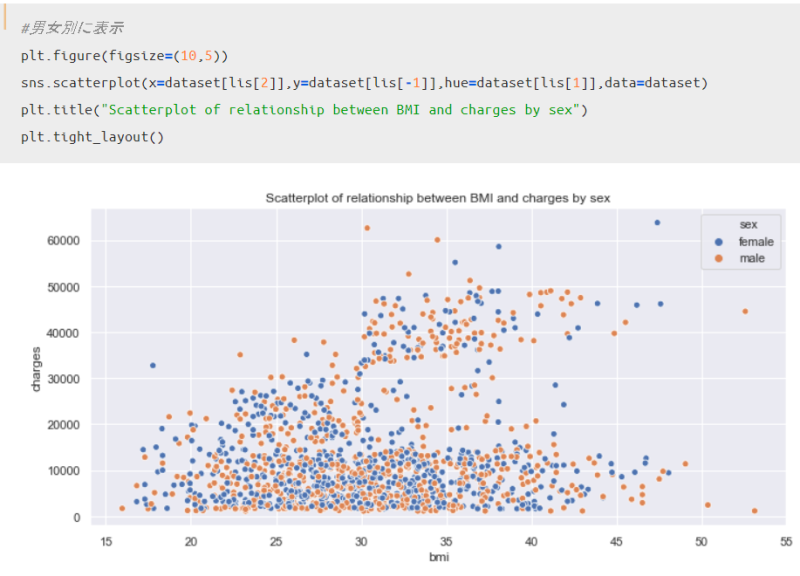
次に、喫煙習慣別に分けて表示した結果が以下です。
この結果を見ると、先ほどの男女別とは明らかに異なり、同じBMI指数でも喫煙者の方がChargeが高い傾向にあることが一目瞭然ですね。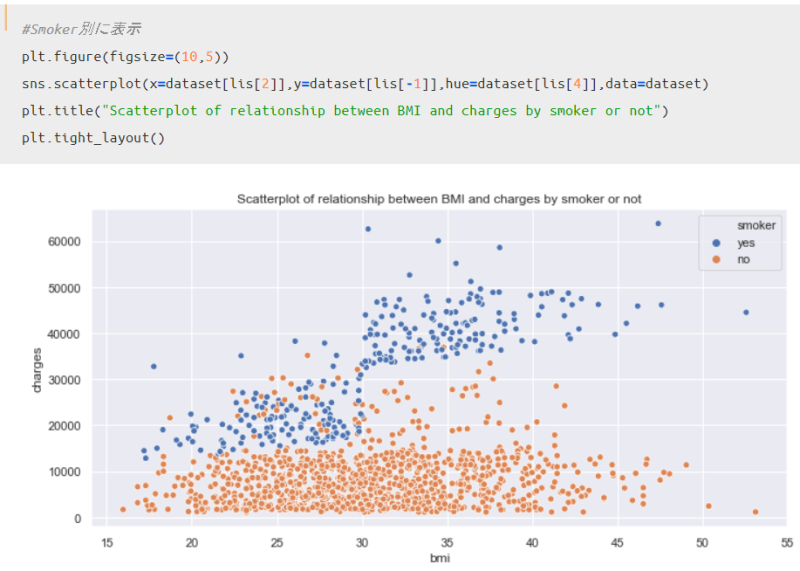
このように散布図を用いてあげることで、無味乾燥なデータから何かしらの法則を見つけることが出来るようになります。コードの基本的な操作を理解した後は、色々なデータに対して可視化する練習をしてみてください。
最後に、喫煙習慣の有無でわけた散布図に対しても回帰直線を描いてみましょう。
sns.lmplotを使えば回帰直線を描けるのですが、少しコードの書き方が特徴的です。
以下のように、dataset[“X”]のように指定した部分は[“X”]とするだけでよい点が先ほどまでと異なります。
(リスト指定ではなく、直接カラム名をしてわかりやすいようにしています。)
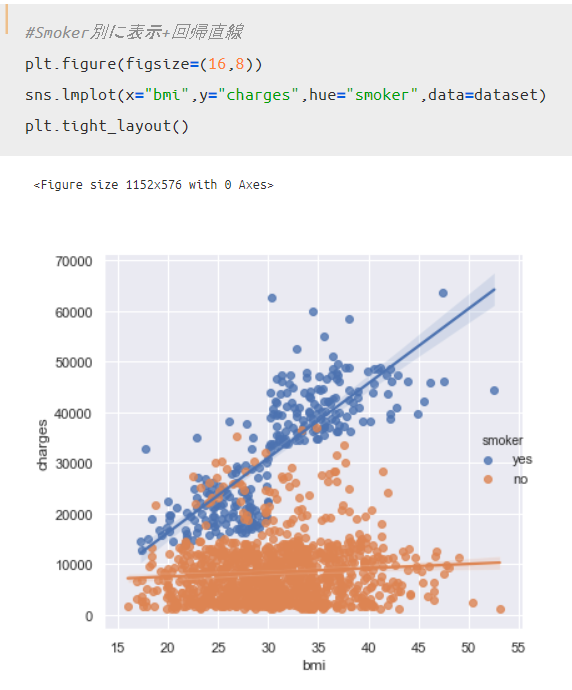
非喫煙者はBMIが向上してもChargeはさほど変わらないのに対して、喫煙者はBMIの向上に応じてどんどんChargeが上昇している傾向にあるのがわかります。
まとめ
いかがだったでしょうか?
今回は可視化手法として「散布図」について紹介してきました。
量的変数同士の可視化をしたい場面で使える手法なので、是非使えるようにしてしてみてください。
では今回はこのへんで。
